Skip to contents

Getting Started

getting_started.Rmd

Loading & viewing your data

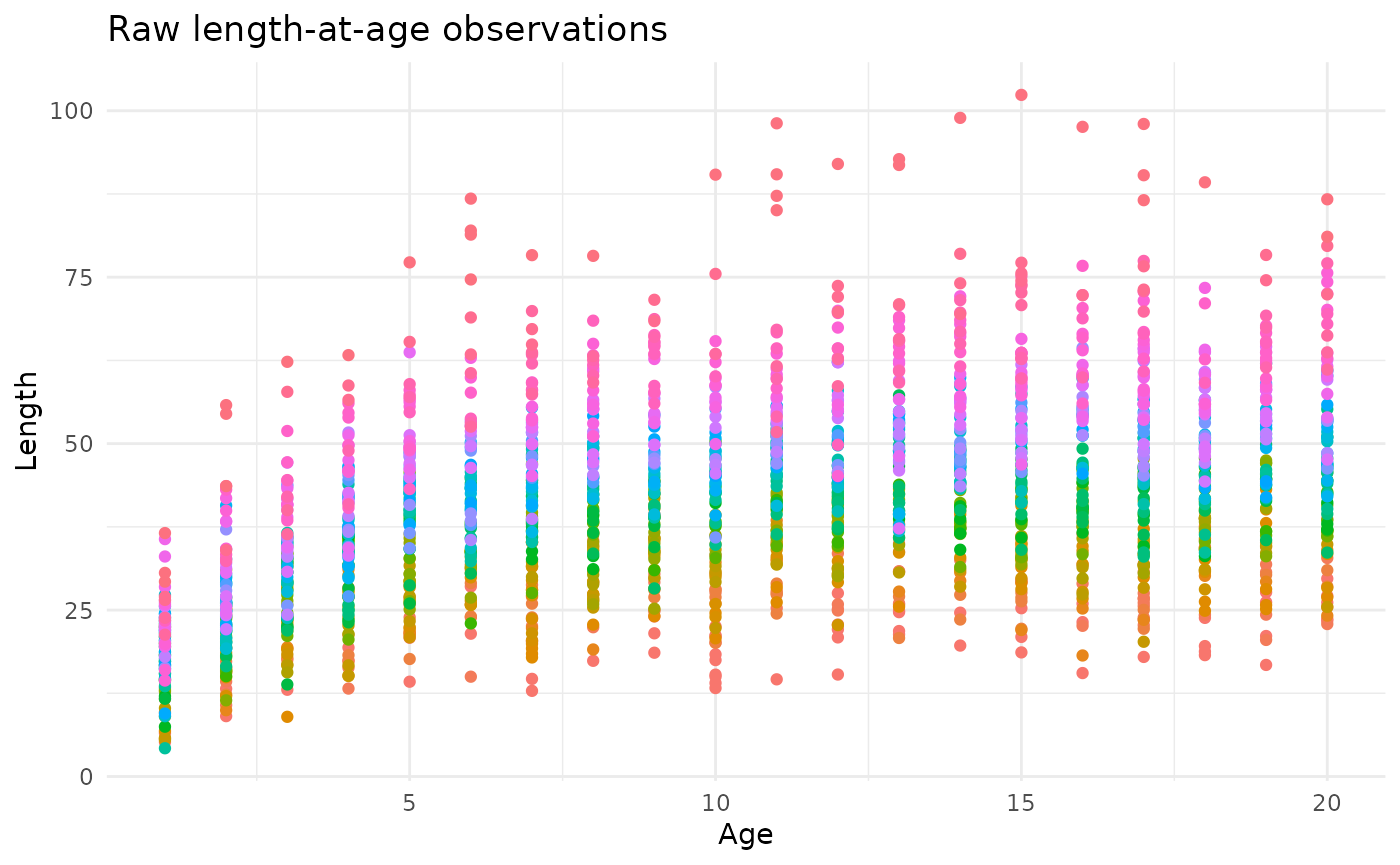
The example shown here will include a simulated spatial process giving rise to heterogeneity in fish length-at-age with a predominant north-south cline.

The first step is to ensure your data are formatted correctly and to be aware of any sample size issues. This is accomplished via check_data(), which returns plots of the observations and residuals.

library(growthbreaks)
data(simulated_data) ## from the package
head(simulated_data)
#>   year age    length      lat      long
#> 2    1   1  5.174880 56.97959 -156.2602
#> 3    1   1  6.532786 57.34694 -142.2419
#> 5    1   2  9.067383 56.61224 -151.8233
#> 7    1   2 13.178737 67.63265 -169.8984
#> 8    1   2 16.415712 55.14286 -169.2174
#> 9    1   2 19.372655 51.46939 -148.3869
p <- check_data(simulated_data, showPlot = FALSE)

The first plot (p[[1]]) shows the input data, colored by year:

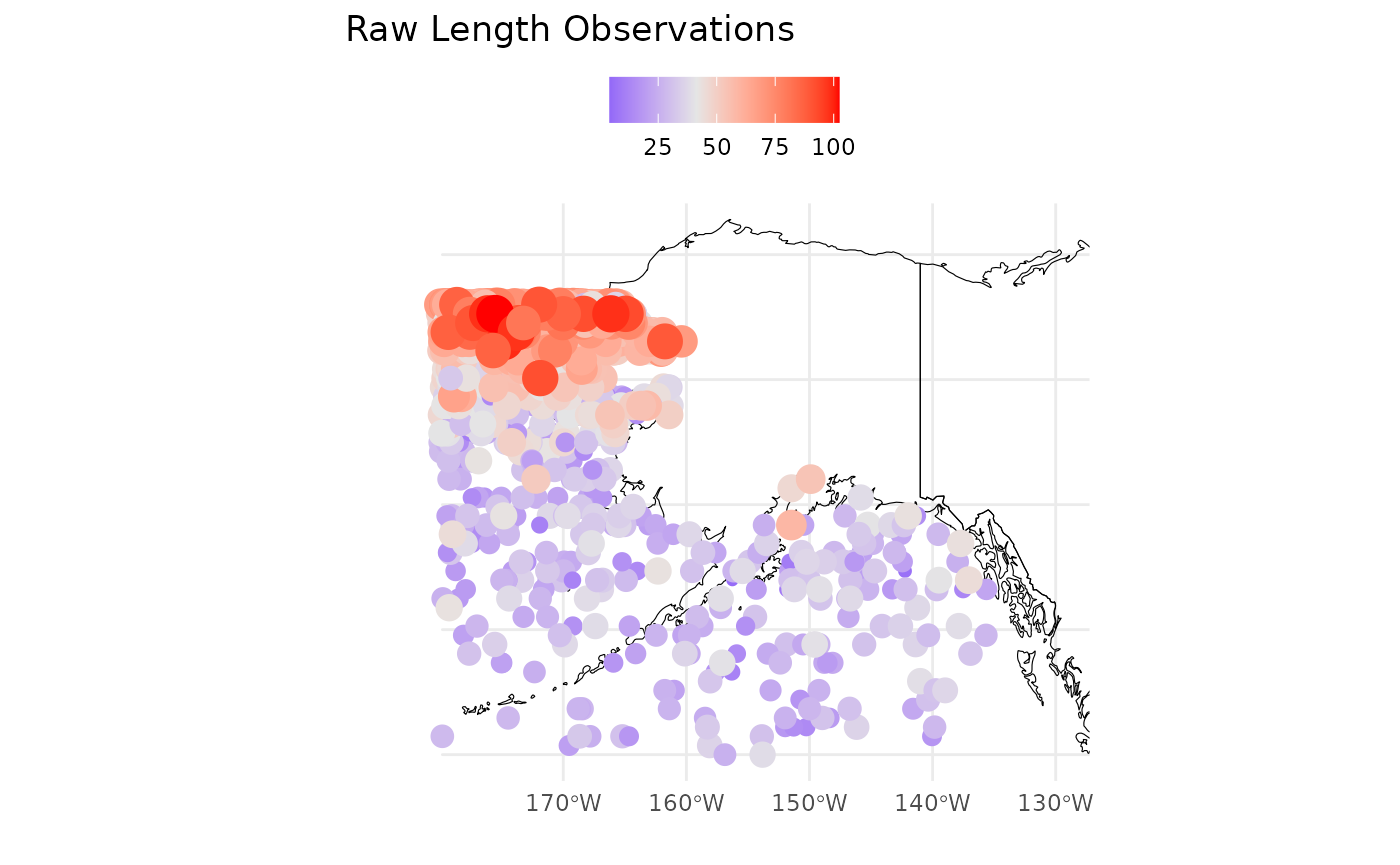
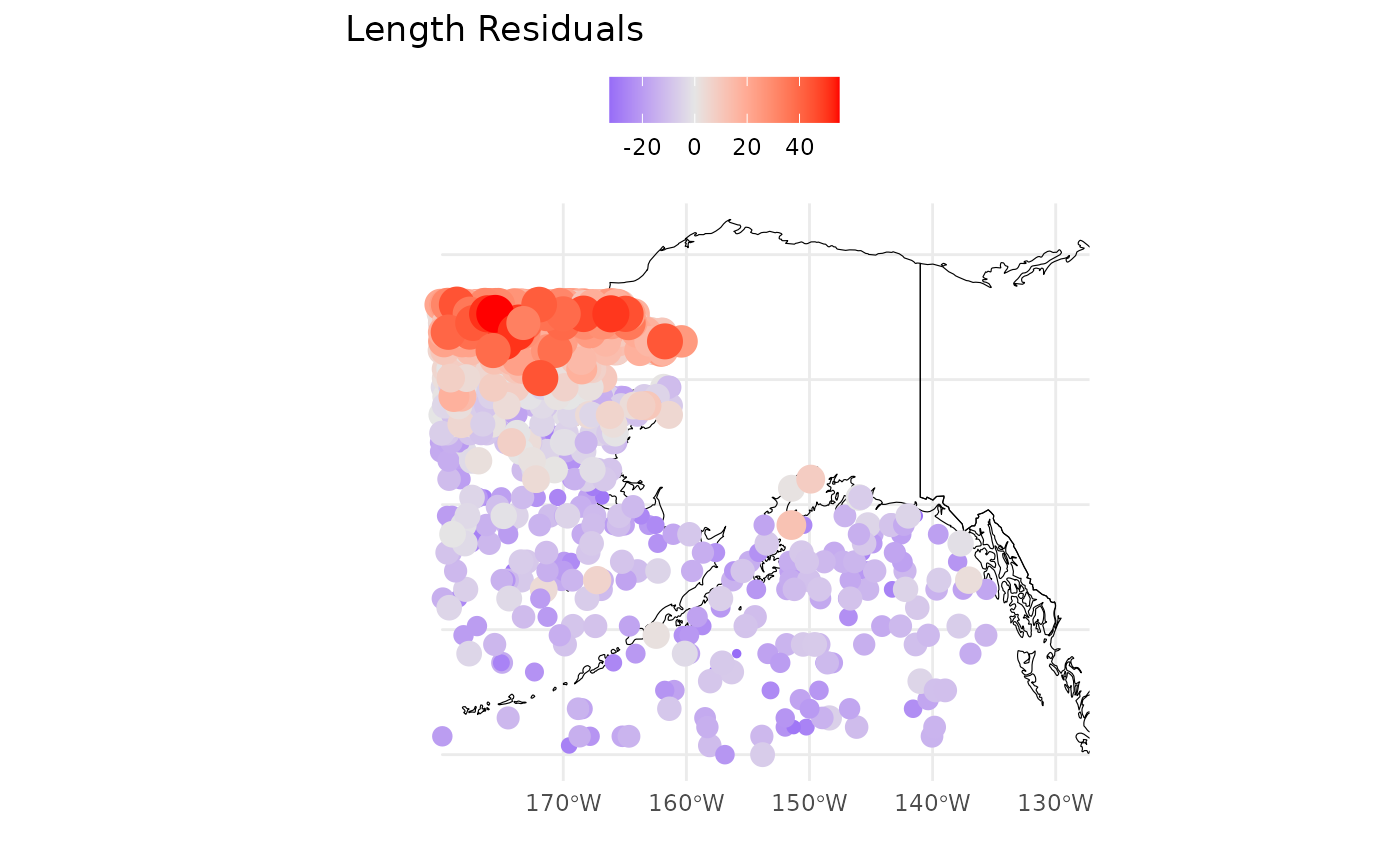
The second two plots p[[2]];p[[3]] are maps of the observations and simple residuals (observation minus age-specific mean). The red colors are the highest values. We’d expect these to look similar to one another.

Once you’ve completed that step you are ready to investigate potential breakpoints in length-at-age via get_Breaks(). This example will use the default option axes = 0 which looks for spatial breakpoints only. The function is ignorant of any underlying structure in the data and is not fitting growth curves at this time. If you keep the default settings you will get back plots of the hypothesized breaks as well as a dataframe with the breakpoints.

Detecting Breakpoints

Now we can pass our data to get_Breaks().

The ages_to_use argument allows you to specify a subset of your age observations for which you’d like to test for breakpoints. If you are unsure, you may choose to use age(s) that are well sampled in your data, or all ages. However, you will want to include at least some observations of small (young) fish, since discrepancies in size may be less obvious for fish at or near their asymptotic length. Here I am testing three ages and saving the output to a dataframe called breakpoints.

breakpoints <- get_Breaks(dat = simulated_data,
                          ages_to_use = c(5,10,15),
                          sex = FALSE, 
                          axes = 0, 
                          showPlot = TRUE)

breakpoints
#>         lat      long detected_break      freq
#> 87 65.63636 -141.4534           TRUE 0.3333333

As we might have expected based on the raw observations, the algorithm detected a break at about 66∘66^{\circ}N, as well as an unexpected one at 141∘~141^{\circ}W. We can see this on the map as well as in the dataframe. The count column indicates the proportion of tested ages for which this breakpoint was detected (in this case, 1/3, suggesting that no breakpoints were detected for 2/3 ages). You may choose to stop here. If you’re interested in some of the automated checking and curve fitting functionality, proceed to the next step.

Re-fitting growth curves at putative breaks

The function refit_Growth() can be used to generate plots of the growth parameters and associated curves by splitting your data into the spatio/temporal zones (“strata”) defined by breakpoints. This can allow you to make inferences about a) the magnitude and significance of differences in individual parameters and b) the resultant impact on our perception of length-at-age.

It is common for growth curves to be very similar especially when the number of strata is large (>3), so user judgment is required to discern the best use of the information provided here.

Run the function with the breakpoints as-is and inspect the outputs.

fits1 <- refit_Growth(simulated_data, breakpoints, showPlot = FALSE)

names(fits1$split_tables) ## description of the strata used
#> [1] "lat_less_66_long_less_-141"    "lat_greater_66_long_less_-141"
#> [3] "lat_less_66_long_greater_-141"
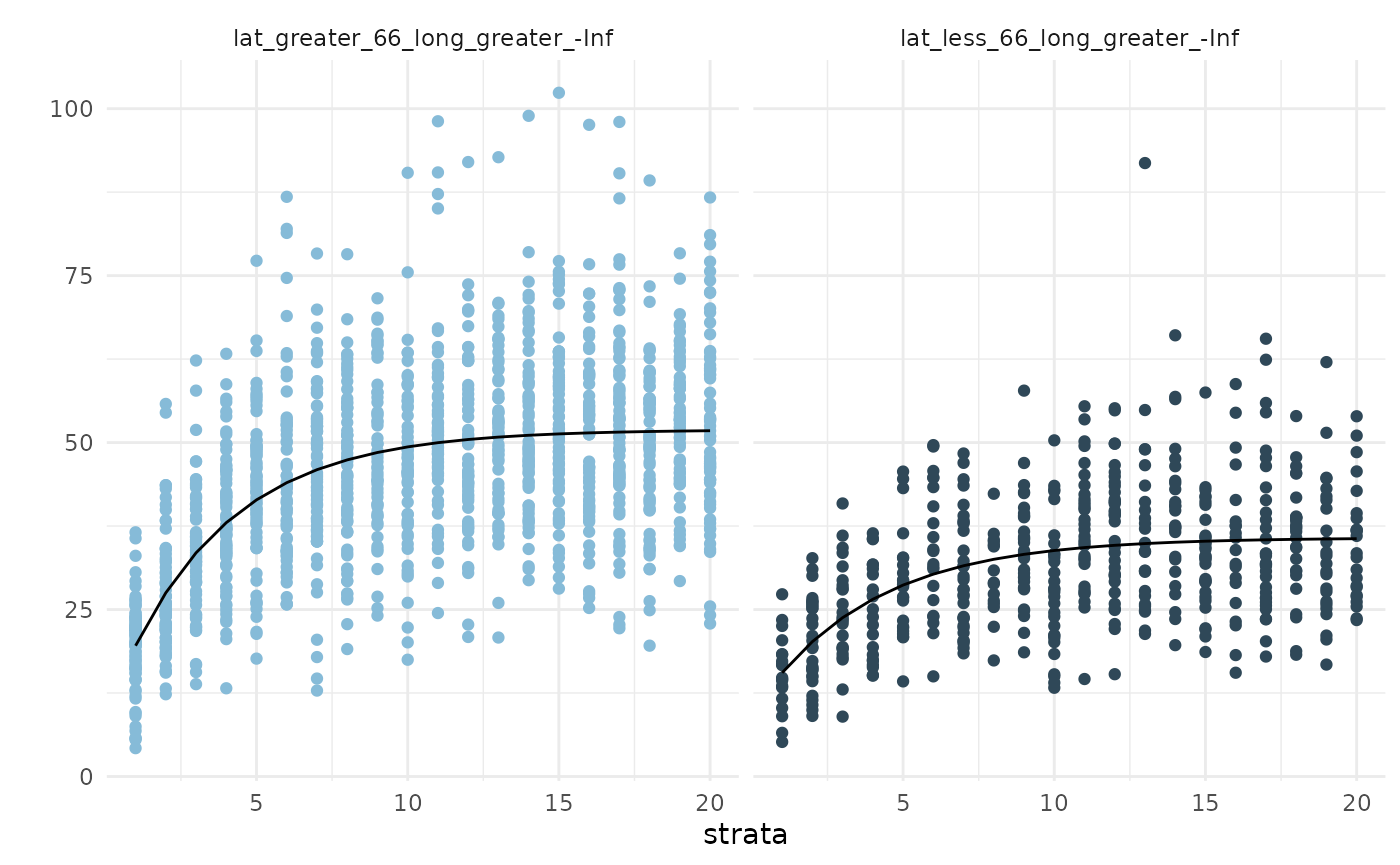
## split_tables contains your observed data broken up by strata

We can inspect the fitted curves in two ways: first, by visualizing the $par_plot. The red points & error bars indicate estimates for which the mean fell outside the confidence interval(s) for other strata. This can be used to infer which components of the growth curve are possibly contributing to detected differences among strata. It doesn’t look like the second strata’s L∞L_{\infty} nor kk values are very different than the other regions’.

fits1$pars_plot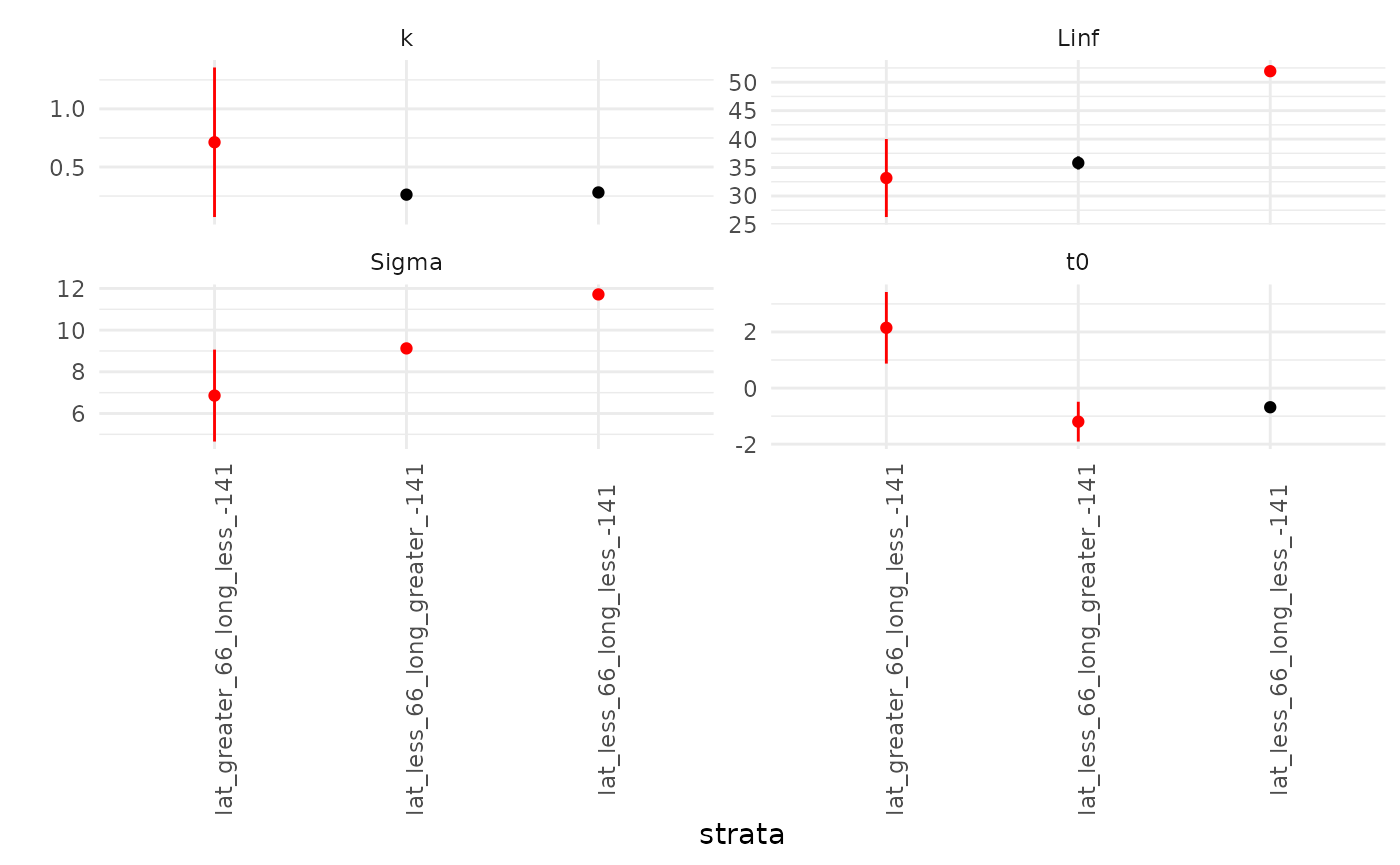

The second way to explore the results are by visualizing the fitted curves against the strata-specific observations contained in $fits_plot. Here we see that the second and third strata (all data points below 66∘66^{\circ})N exhhibit very similar curves, and there are not many data points in the second strata to begin with.

fits1$fits_plot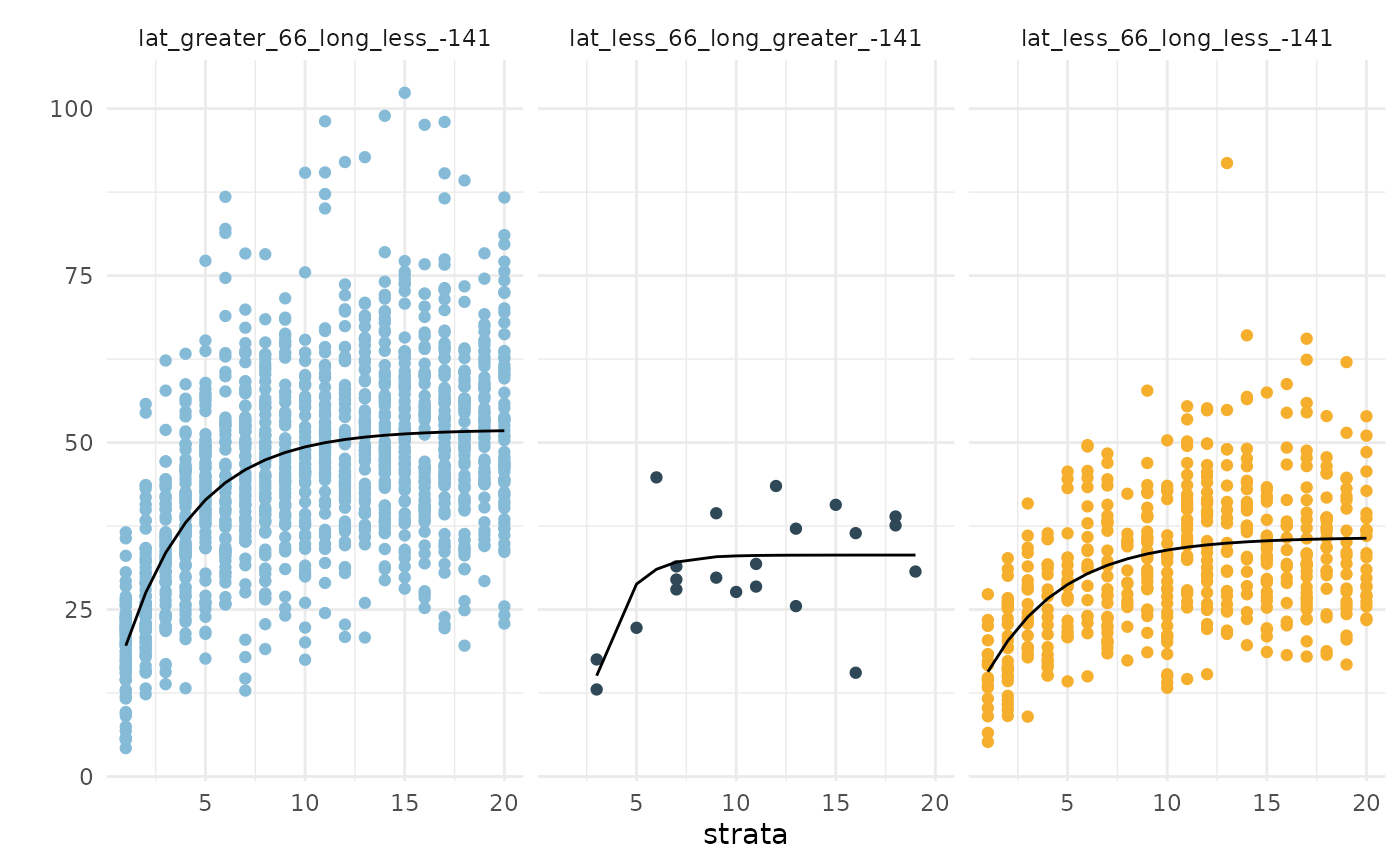

Updating and re-fitting the breakpoints

Based on the exploration above, you may decide to manually combine the second and third strata, using just a single breakpoint north to south. In this case, we would do away with the breakpoint at −141∘-141^{\circ})W, replacing it with -Inf.

breakpoints$long <- -Inf 
fits2 <- refit_Growth(simulated_data,
                      breakpoints,
                      showPlot = FALSE) ## refit the curves

We can repeat the visualization and see that 1) the key parameter values are now more distinct from one another and 2) so are the curves.

fits2$pars_plot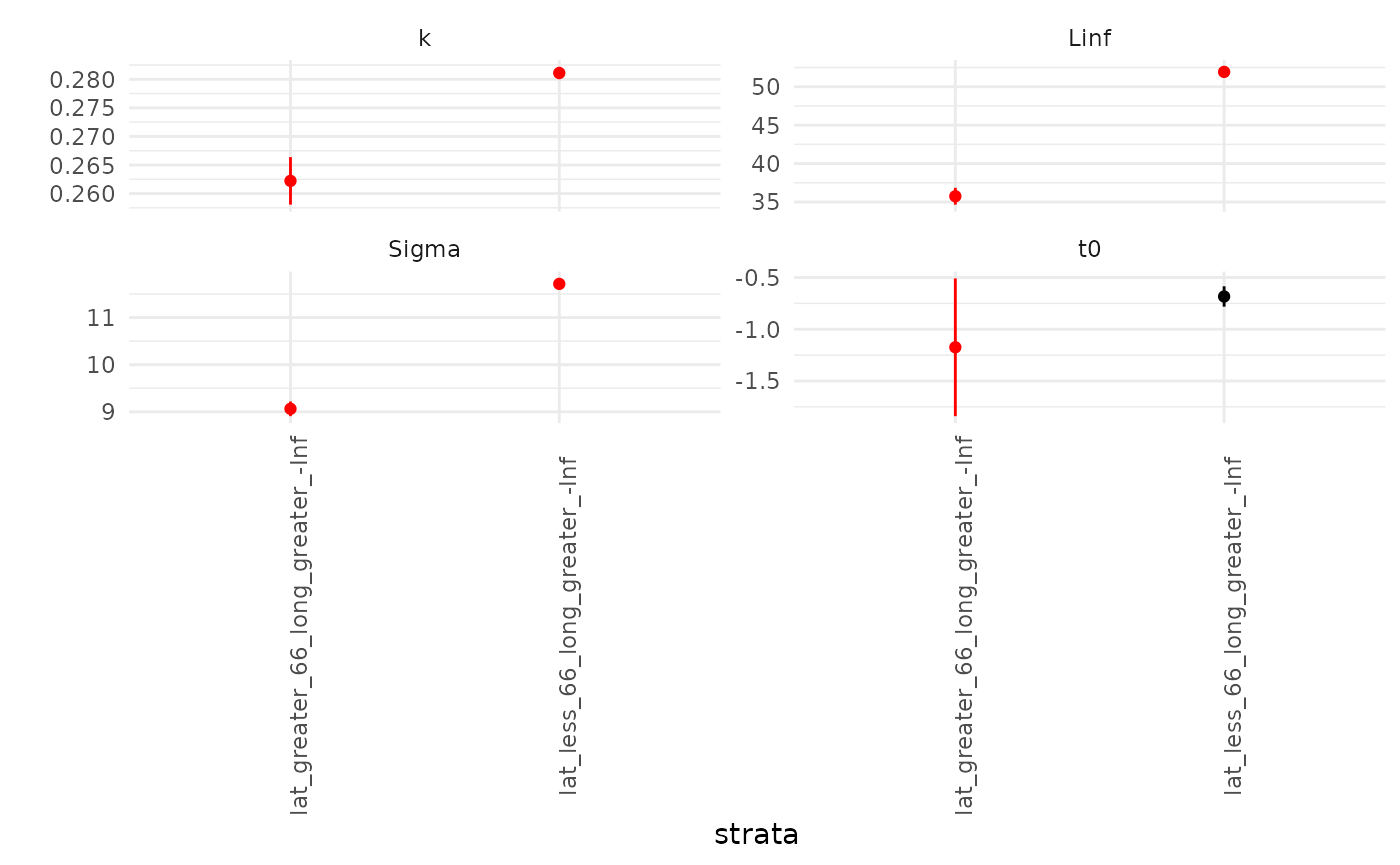

fits2$fits_plot